Ashby法

製品マップとAshbyマップ

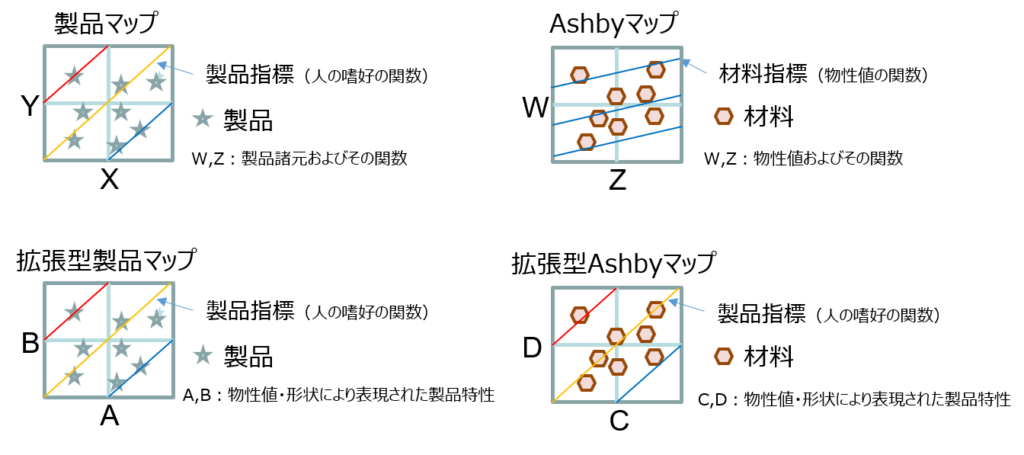
Ashby法ではAshbyマップを、1DCAEでは製品マップを設計のものさし（指針）として使用します　Ashbyマップが材料を、製品マップが製品を対象としている点を除いて、両者は共通性が多く、Ashby法と1DCAEを連携させることによって、新たな製品開発手法が提案できるのではと考えています　ここでは、製品マップとAshbyマップに関して、その定義を確認するとともに、製品マップの例を通して、今後の課題にも触れます

Ashby法視点でのDelight設計

Ashby法では材料・プロセスを設計の重要な要素と考え、最初に材料・プロセスを決めるのではなく、設計というプロセスを通して柔軟かつ合理的に材料・プロセスを決定していくことを特徴とします　この考え方は材料・プロセス以外の要素も対象とする機械設計に広く適用できます　この橋渡しをするのが1DCAEです　ここでは、Ashby法視点での設計、特にDelight設計について紹介します

Ashby法と1DCAEによる設計の基本概念

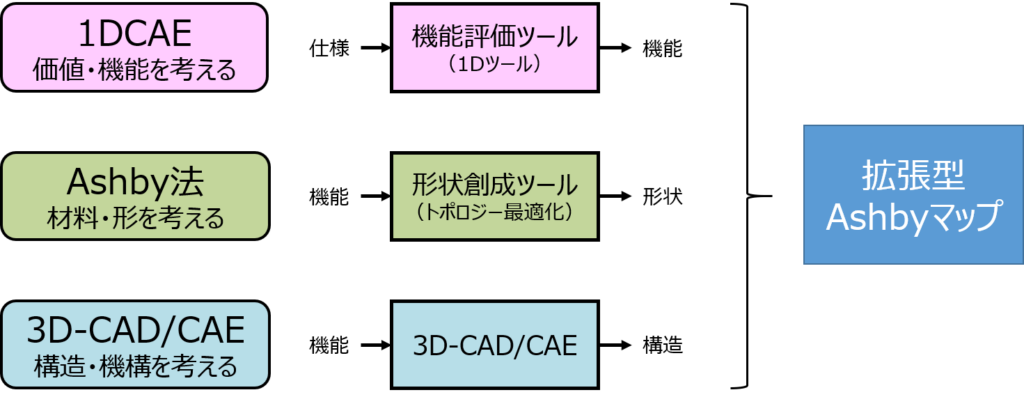
Ashby法と1DCAEによる設計が目指すところを今一度、考えるとともに、1DCAEの構成と効果を若干詳しく説明します　これらを受けて、Ashby法で使用するAshbyマップと1DCAEで使用する製品マップとの関係を価値／機能／構造の視点で事例も交えて明らかにします　最後に、Ashby法を実際に機械設計に適用するにあたって、不可欠な拡張型Ashbyマップの考え方、作成手順を紹介します

Ashby法と1DCAEによる価値創造プロセス

価値創造プロセスを実現するために、Ashby法と1DCAEの連携を考えます　最初にものづくりの変遷を紹介、これを通してものづくりの対象が拡大していることを示します　次にひとの行動パターンから見たものづくりの目指すところを考えます　これらを受けて、Ashby法と1DCAEによる価値創造プロセスを提唱します　最後に適用事例を紹介します

材料と形状の選定法の具体例

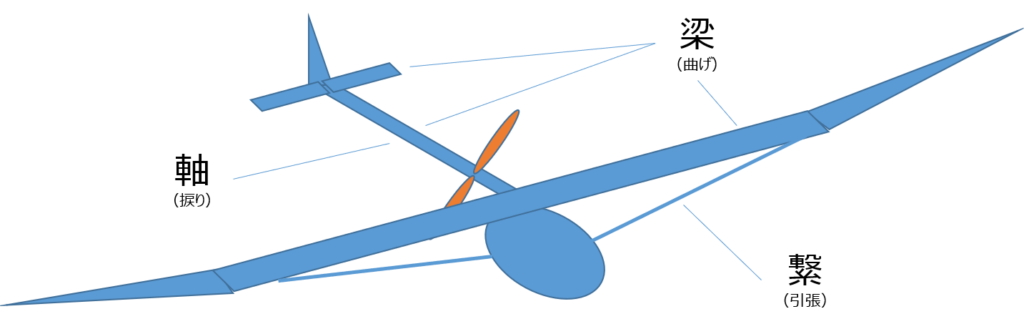
材料と形状の選定法の具体例への適用方法を紹介します　最初に、種々の構造／荷重に対する形状指標を用いて、重量最小化を設計問題とした場合の形状を考慮した材料選定のための剛性ならびに強度に関する設計指標について述べます　この適用例として、人力飛行機の主翼の形状を考慮した曲げ剛性設計例（軽くて剛な梁）について述べます　また、Ashbyマップを用いて形状を考慮した軽くて剛な梁を具現化する材料を選定する方法について述べます　最後に、テーブルの脚の材料と形状を決定する設計問題の実施手順について説明します

曲げ強度、ねじり強度に関する形状係数

曲げ強度とねじり強度に着目し、これらに関する形状係数の導出方法を紹介するとともに、梁の曲げ、軸のねじりの断面係数および強度に関する形状係数について説明します　さらに、柱の座屈強度にも言及します

曲げ剛性、ねじり剛性に関する形状係数

形状が具体的にどのように剛性に影響するかについて述べるとともに、この影響を示す指標である形状係数について触れます　次に、梁の曲げ剛性、形状係数に続いて、軸のねじり剛性、形状係数の導出方法を紹介します以上の結果を受けて、代表的な断面形状を有する梁の曲げ、軸のねじりのモーメントおよび形状係数について説明します

材料と形状の選定手順の基本概念

材料から形状を導出するプロセスそのものが機械設計と言えますが、Ashby法ではこの際に種々の材料の特性を可視化することにより、適切な材料選定を行うことを特徴とします　そこで、材料から形状への変換プロセスを説明し、設計を行う際に重要となる荷重の形態とこれに関係する形状因子について考えます　荷重形態のうち、梁の曲げに着目し、材料と形状の選定手順の基本的概念を紹介します

材料・プロセスの基礎知識と機械設計

材料および加工プロセスと機械設計の関係について多面的に考えるとともに、材料、加工プロセスの分類例を紹介します　機械設計は機能を形状に変換することにより製品として具現化するプロセスで、この際にはその源となる材料および材料を形状に変換する加工プロセスが重要となります　この意味で、材料および加工プロセスの詳細を理解しておくことは実際にAshby法を機械設計に適用する際の基本となります

蓄熱壁の設計問題とAshby法

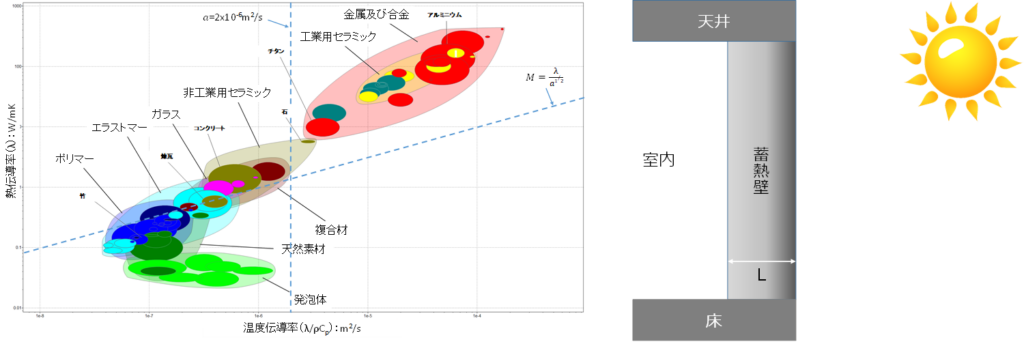
太陽熱を利用した蓄熱壁の設計問題について考えます本　最初に太陽熱を利用した蓄熱壁について説明します　つぎに、太陽熱を利用した蓄熱壁の設計問題を考えるにあたって必要となる伝熱の問題を振り返り、必要となる基礎式を導出します　この式より、材料選定に際の指標を導き、設計のための材料指標を導出、この結果をAshbyマップ上に表現、太陽熱を利用した蓄熱壁に適切な材料選定に関しての検討を行います

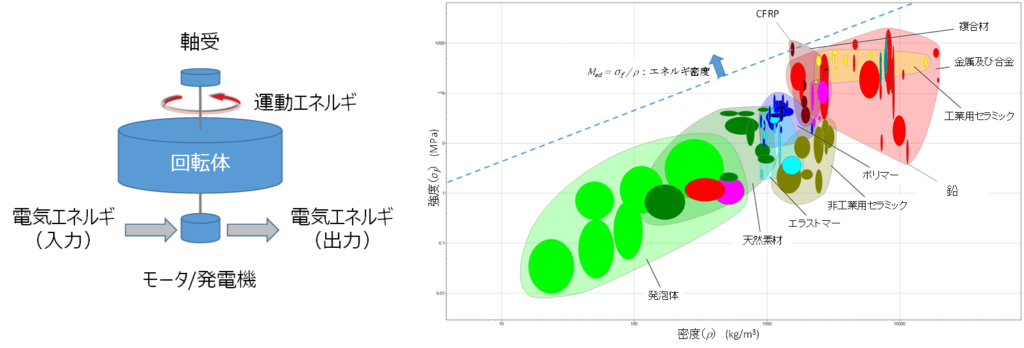
フライホイールの設計問題とAshby法

フライホイールの設計問題について考えます　最初のフライホイールについて説明します　フライホイールには様々な用途がありますが、ここではその回転の運動エネルギを利用した発電を目的としたフライホイールを対象とします　フライホイールの設計問題を考えるにあたって必要となる回転エネルギの導出方法、発電用フライホイールの最大の制約である回転時の応力の導出方法について説明します　これらの知見をもとにフライホイールの設計問題を考えます

テーブルの椅子の設計問題とAshby法

テーブル・椅子の足の設計問題について考えます　テーブル・椅子の足はものを置いたり、人が座ったりするために十分な強度を有している必要があります　また、使用上の制限より、軽くてスリムなことが要求されます　一方、テーブル・椅子の足のようにスリムな構造においてはその強度に耐える力より小さい力でも足が変形してしまう座屈という現象が発生します　そこで、最初にテーブル・椅子の足と座屈という現象について紹介した後、座屈という現象の定式化を行います　この定式化の結果を具体的に理解して貰うために簡単な実験を行います　以上の結果を受けて、テーブル・椅子の足の設計問題を考えます

Ashby法に関するワークショップ参加報告@ケンブリッジ（2017年4月）

4月4日～7日にAshby法に関するシンポジウムならびにワークショップが英国ケンブリッジで開催されましたので報告します

Ashby法に関するワークショップ参加報告@シンガポール（2016年12月）

12月8日～10日にシンガポールのNUS（シンガポール国立大学）でAshby先生が主宰する会議があり、先生とお会いして議論する機会を得たので報告します

ボートのオールの設計問題とAshby法

ボートのオールの設計について考えます　最初に設計のシナリオについて基本問題で学んだ手順も踏まえて、オール材料の選定手順に関してAshbyマップを元に説明します　次に、ボートのオールの設計問題をより一般的な設計問題として考えます

弾性体振動とAshby法

振動問題を例に弾性体の振動設計問題を考えます　最初に、“弾性”に関して基本から考え、慣れ親しんでいる縦弾性係数(E)、横弾性係数(G)、ポアソン比(ν)の物理的意味を理解します　弾性体の振動の基本振動形態として縦振動、捩り振動、横振動を、また、基本形状として梁、板を考えます　これらを通して、弾性体の振動が大きく二種類の形式で表現できることを示し、最終的にAshbyマップで表現します

熱問題とAshby法

熱設計問題を例にAshby法の適用手順を紹介します　材料・プロセス選定と熱設計を考える上で重要なのが熱の性質の理解です　これは一般には“伝熱工学”という専門領域が該当します　ただ、ここでは、設計の視点から、1DCAEの考え方に沿って、熱とは何かから初めて最終的には周知の関係式、特性値にたどり着きます　次に上述の熱に関係する式、特性値を起点として熱設計に関する諸問題をAshby法で解きます　熱を通し易い材料／通し難い材料、熱は通すが電気は通さない材料、精密機器で熱の影響を受けにくい材料、熱特性とコスト、重量を両立した材料、触って暖かく／冷たく感じる材料について考えます

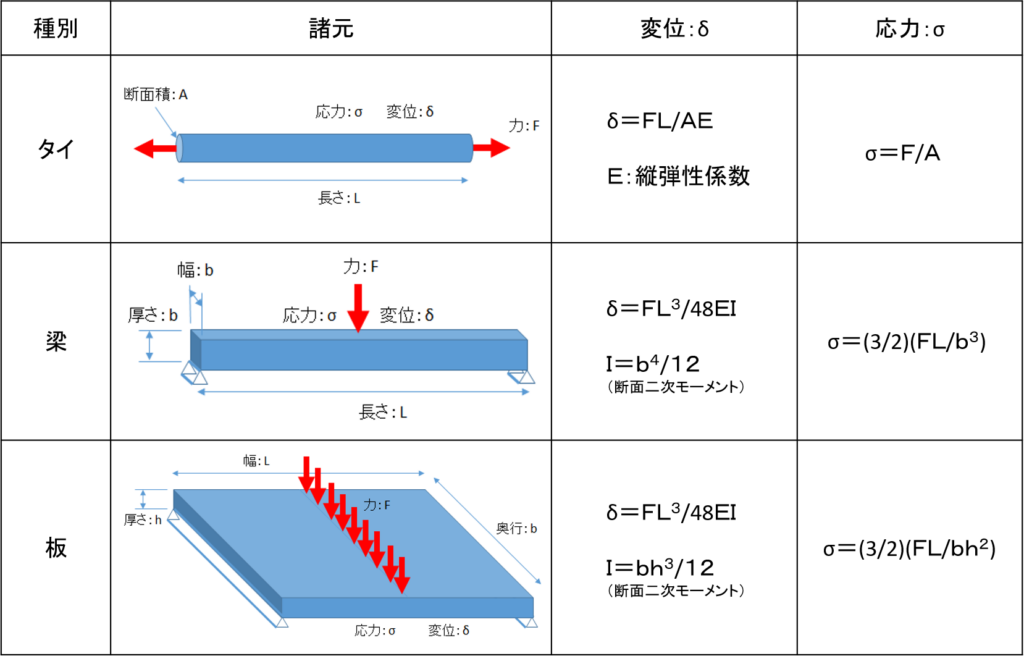
材料力学の基礎知識とAshby法

Ashby法では（1DCAEでも）対象とする問題の本質を的確に捉え、見通しの良い形式でシンプルに表現することが基本となります　そこで、最初に材料力学の知見を元に上記三種類の基本構造の変位、応力を求める式の説明を行います　この結果を受けて、“軽い構造物”という設計問題を三種類の基本構造に関して、“十分な剛性を有している”と“十分な強度を有している”の二種類の制約条件下で解き、設計指標を導出します　最後に、この設計指標をAshbyマップで表現します

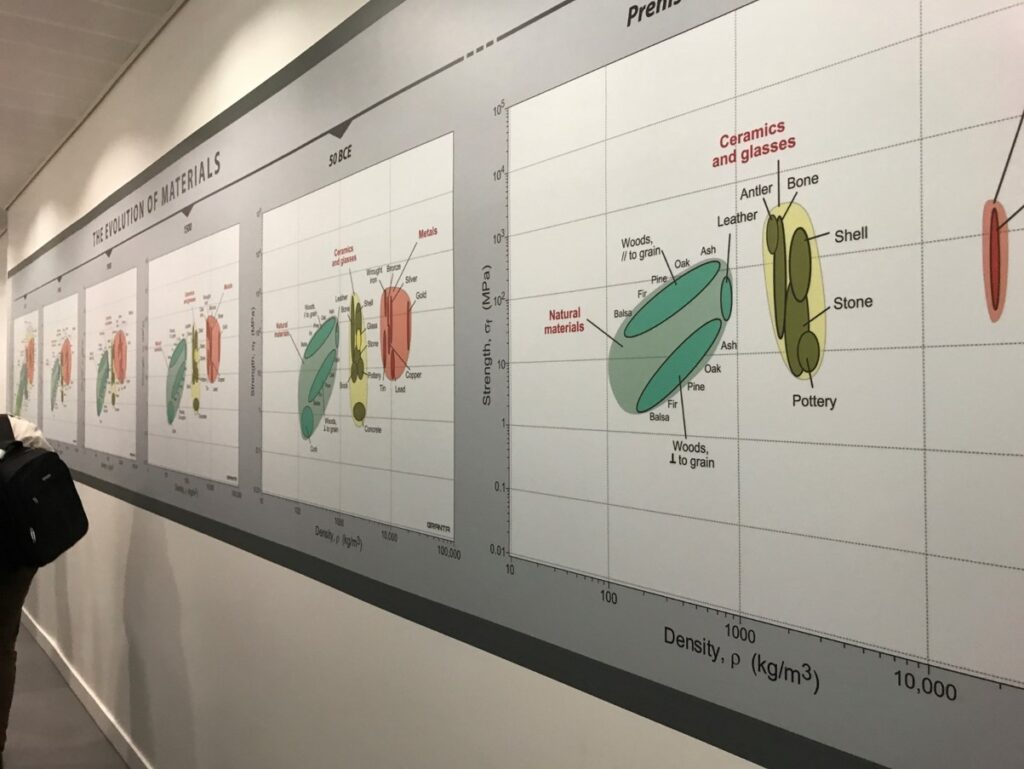
Ashby法とは

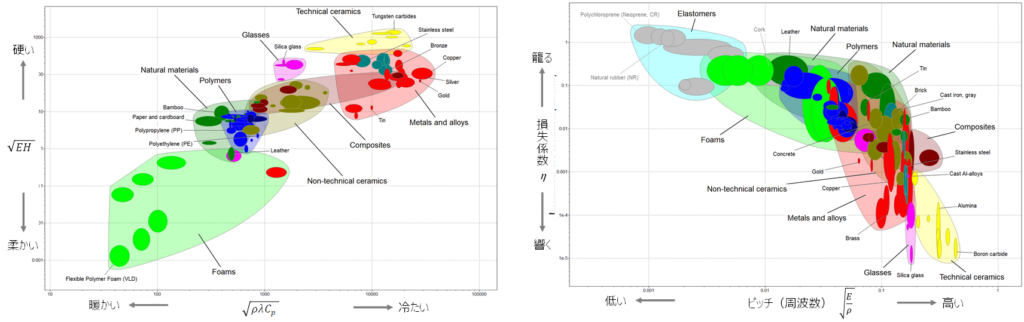
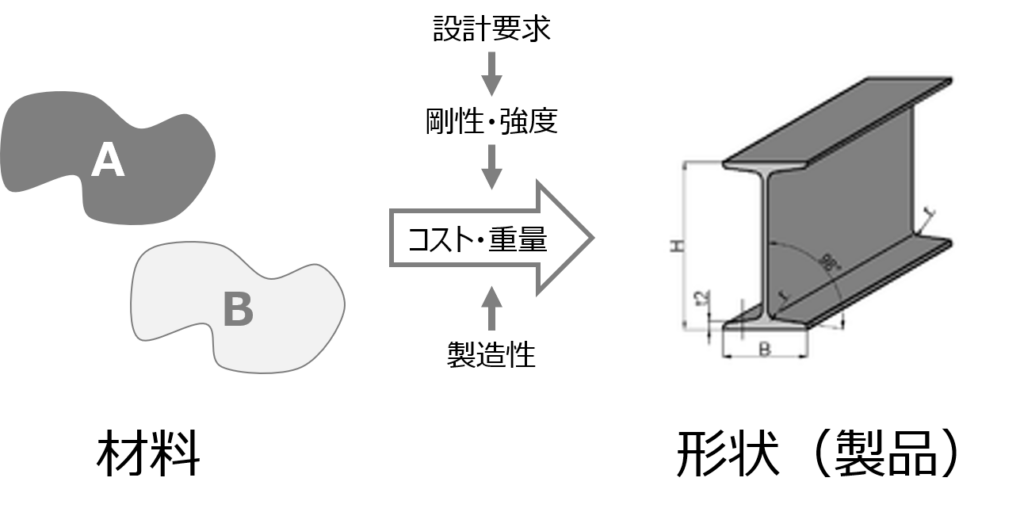
Ashby法の出発点となるのは材料・加工プロセスデータ、すなわち、材料物性、エコ属性、感覚属性、接合プロセス属性、表面処理プロセス属性、成型プロセス属性です　これらは連続量、離散量、等様々な形式で表現されます　一連の材料・プロセスデータから二つのデータを選択して二次元マップを作成、このマップ上に該当する材料・プロセスをプロットしたのが材料・加工プロセスマップです　また、加工プロセスマップの場合には加工プロセスデータを一軸に、もう一軸に加工プロセスの種類をとる場合もあります　一方、設計問題として例えば、軽くて十分な剛性を有する梁を考えます　この場合、“軽くて十分な剛性を有する梁”という設計目標において、十分な剛性を有するという制約条件下で質量を目的変数として最小化するという設計問題に置き換えることができます　この設計式は設計指標として、二つの設計変数（材料物性及び材料・プロセス属性）の関数で表現できます　この関係を材料・加工プロセスマップ上にプロットしたのがAshbyマップです

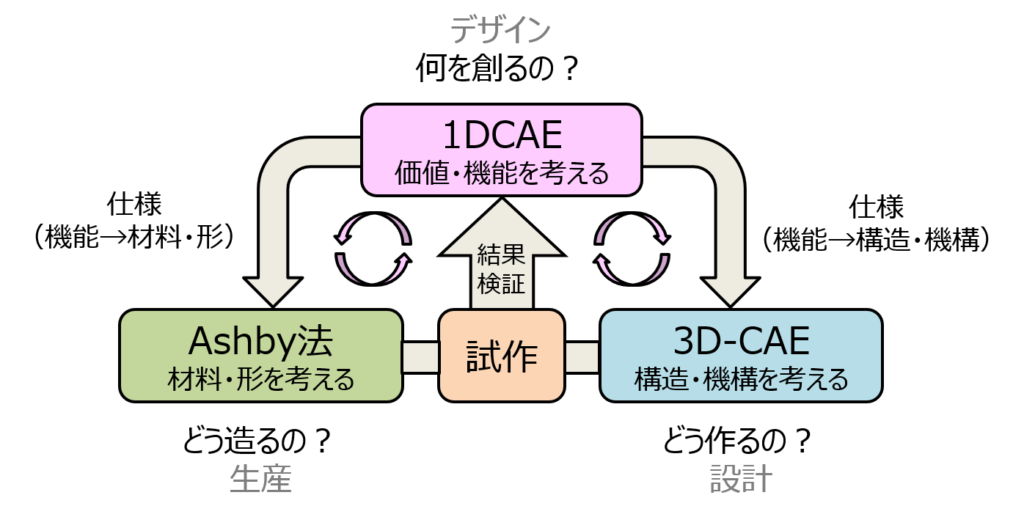
Ashby法と1DCAEによるものづくり

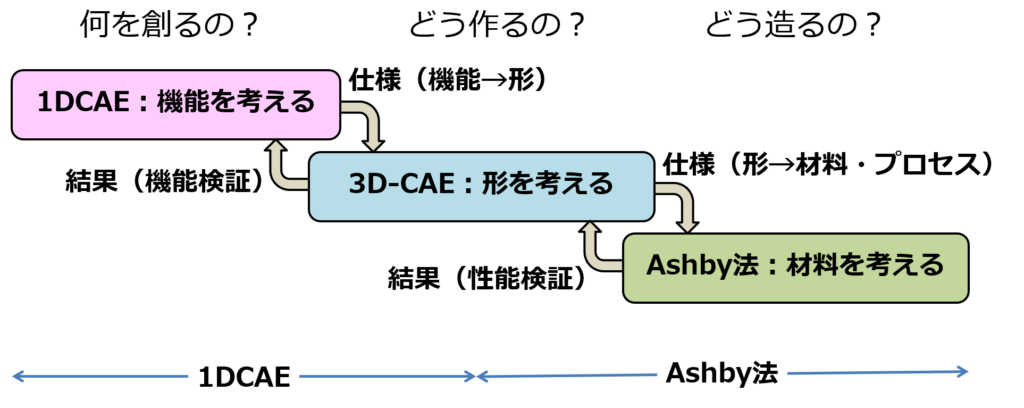
Ashby法と1DCAEによるものづくりについて説明します　1DCAEで“何を創るか”を決め、3D-CAEで“どう作るか”を決め、Ashby法で“どう造るか”を決めます　1DCAEで考えた（定義した）機能は設計仕様として3D-CAEに渡されまする　3D-CAEではこの仕様に基づいて形を考えます　この結果は1DCAEに反映され、機能を検証します　ここまでが1DCAEの流れです　次に、3D-CAEで考えた形がAshby法に渡されます　Ashby法ではこの仕様に基づいて材料・プロセスを決定します　この結果は3D-CAEに戻され、性能を検証します　Ashby法は機械設計の基本問題を起点に材料・プロセスの選定問題に落とし込む一連の設計プロセスですので、3D-CAEとAshby法をセットでAshby法と考えることができます　これは1DCAEが3D-CAEとセットで1DCAEと考えるのと同じです